แจกฟรีแนวข้อสอบวิศวกรไฟฟ้า กฟผ

แนวข้อสอบวิศวกรไฟฟ้า

1.         กำหนดให้ รีเลย์ A และ B มีการทำงานแบบ Standard Inverse Time Relay โดยเวลาที่ใช้ในการตัดวงจรเป็นดังสมการ      t  =       โดยที่ 

  เป็นค่ากระแสผิดพร่องที่รีเลย์วัดได้

               เป็นค่ากระแสปรับตั้ง

t  เป็นเวลาที่ใช้ในการตัดวงจร

จงคำนวณหาค่า TMS ของรีเลย์ A ในรูป  กรณีที่ต้องการใช้เป็นการป้องกันสำรอง (Backup Protection) ให้กับ รีเลย์ B โดยมีช่วงเผื่อ (Margin) ของการทำงานมีค่าเท่ากับ 0.4 วินาที

1) 0.05                                                               2) 0.10

3) 0.15                                                               4) 0.20

เฉลย ข้อ3

วิธีทำ

               การปรับตั้งรีเลย์ A

                              กระแสปรับตั้งด้าน Secondary(Is) = 5 A

                              ดังนั้นกระแสปรับตั้งทางด้าน Primary = 100 A

                              จะเห็นว่า  I_{F MAX}   =            1400 A

                              ดังนั้นค่า PMS = 1400/100 = 14

จากกราฟ Standard Inverse(SI)  t =       ที่ TMS = 1.0

t =      = 2.58 s            ที่ TMS = 1.0  

เนื่องจากรีเลย์ A อยู่ใกล้ Fault มากที่สุดจึงปรับตั้งเวลาทำงานให้น้อยที่สุดเพื่อให้ทำงานเร็วที่สุด จึงเลือก TMS = 0.05

ดังนั้น

                              Operating Time ของลีเลย์ = 2.58x 0.05 = 0.13 s

การปรับตั้งรีเลย์

                              กระแสปรับตั้งทางด้าน Secondary (I_s)        =             5  A

ดังนั้น

                              กระแสปรับตั้งทางด้าน Primary = 200 A

จากค่า

                              I_{F MAX} = 1400 A

            ดังนั้น                                                                     

                              PMS      =    = 7

จากกราฟ Standard In (SI)  t  =   = 3.60 s  ที่  TMS = 1.0

เนื่องจากเวลาทำงานของรีเลย์  B  ต้องเผื่อ  Margin 0.4 s

ดังนั้นเวลาการทำงาน = 0.13 + 0.4 = 0.53 s

ดังนั้น TMS =   = 0.147

เพราะฉะนั้นเลือกใช้ TMS = 0.15

 

2.         กำหนดฟังก์ชันต้นทุนเชื้อเพลิงของเครื่องกำเนิดไฟฟ้า 2 ยูนิตดังนี้

 Bath

 Bath

โดยที่ P1 และ P2 มีหน่วยเป็น MW หากโรงงานไฟฟ้าดังกล่าวจ่ายโหลด 450 MW จงจัดสรรกำลังผลิตตามหลักเศรษฐศาสตร์

1) P1 = 200 MW และ P2 = 250 MW                         2) P1 = 250 MW และ P2 = 200 MW

3) P1 = 300 MW และ P2 = 150 MW                         4) P1 = 350 MW และ P2 = 100 MW

เฉลย ข้อ 3

วิธีทำ

จากสมการ

 Bath

 Bath

ทำการหาอนุพันธ์จะได้

 (0.005+2+100)  -----------------------------------()

λ  =  2 + 0.01

 (0.001+2+200)  -----------------------------------()

λ  =  2 + 0.02

จะได้

λ  =  2 + 0.01 =  2 + 0.02

เพราะฉะนั้น

+ = 450

แก้สมการเพื่อหาค่า    และ    จะได้

  =  300 MW

  =  150  MW

 

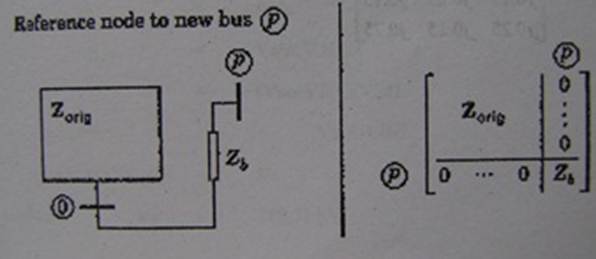
3.         ถ้านำค่า Impedance ที่มีค่า j0.5 มาต่อที่ bus1 ไปยัง bus3 ซึ่งเป็น bus ใหม่ จงหา Zbus ใหม่ เมื่อกำหนด Zbus เดิม  ดังนี้

 

 

1)           2) 

 

 

 

3 )          4 )

 

 

 

เฉลย ข้อ 2

วิธีทำ

 

 

 

 

 

 

 

 

 

4.         ถ้านำค่า Impedance ที่มีค่า j0.5 มาต่อที่ bus1 (บัสเก่า) ไปยัง reference bus จงหาค่าของ Zbus ใหม่ เมื่อกำหนด Zbus เดิม ดังนี้

 

 

1)        2)

 

 

3) 4)

 

 

 

เฉลย ข้อ3

วิธีทำ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5.         ถ้านำค่า Impedance ที่มีค่า j0.5 มาต่อที่ reference bus ไปยัง bus3 ซึ่งเป็น bus ใหม่  จงหาค่าของ Zbus ใหม่  เมื่อกำหนด Zbus เดิม ดังนี้

 

 

1)          2)

 

 

 

3)    4)

 

 

 

เฉลย ข้อ 2

วิธีทำ

 

 

 

 

 

 

 

 

6.         ถ้านำค่า Impedance ที่มีค่า j0.5  มาต่อระหว่าง bus1 กับ bus2 จงหาค่าของ Zbus ใหม่ เมื่อกำหนด Zbus เดิมดังนี้

 

1)  2)

 

 

3) 4)

 

 

เฉลย ข้อ3

วิธีทำ

 

 

 

 

 

 

 

 

7.         สายส่งสัญญาณ 300 km รับภาระเต็มพิกัดที่ปลายทางซึ่งมีระดับแรงดัน 215 kV ถ้าปรากฏว่า การควบคุมแรงดันของสายส่งมีค่า 24.7 % และค่าคงตัววางนัยทั่วไป  ohm และ  mho จงคำนวณหาแรงดันด้านต้านทาง

1) 217.31 kV                                                    2) 218.31 kV

3) 219.31 kV                                                    4) 220.31 kV

เฉลย  ข้อ 3

วิธีทำ

กำหนดให้

                              Vs          =             AVr+BIr Noload Ir=0

                              Vs          =             AVr

                              Vr          =             Vs/A V.R.

                                             =             (Vno-Vfull)/Vfull

0.247*Vfull        =             Vs/A-Vfull

(1.247*215)*0.818           =             Vs

ดังนั้น    Vs          =             219.31 kV

 

8.         ระบบกำลังไฟฟ้า 2 บัสมี Y-บัส กำหนดด้วย Y11 = -j 12.0  Y12 = j3.0  Y21 = j3.0 และ Y22 = -j9.0 จงกำหนดสมาชิกในตำแหน่ง Z12 ของ Z-บัส

1) j 0.0101                                                        2) j 0.0202

3) j 0.0303                                                        4) j 0.0404

เฉลย ข้อ3

วิธีทำ

                              -j3 / (-99)

 

9.         สายส่งในระบบ 3 เฟส 69 kV มีความยาว 20 km มีค่าอิมพีแดนซ์อนุกรมเท่ากับ 4+j 10 โอห์ม หากด้านรับมีโหลด 50 MVA ตัวประกอบกำลัง 0.8 ล้าหลัง และแรงดันด้านรับมีค่า 65 kV จงคำนวณหาแรงดันด้านหลัง

1) 68.2                                              2) 70.2

3) 72.2                                              4) 74.2

เฉลย ข้อ3

วิธีทำ

 

 

 

 

 

 

10.    จากข้อมูลที่กำหนดให้จงคำนวณหาค่ากระแสไฟฟ้าหลังเกิดฟอลต์ระหว่างบัส  1 และ 3 เมื่อเกิดฟอลต์แบบสมมาตรที่บัส 4 เมื่อแรงดันไฟฟ้าก่อนการเกิดฟอลต์เท่ากับ 1 pu มุม 0 องศา  และอิมพีแดนซ์ระหว่างบัส  1  และ  3  เท่ากับ  j0.25 pu

1) j0.2044                                                                        2) j0.4044

3) –j0.2044                                                                      4) –j0.4044

เฉลย  ข้อ3

วิธีทำ

กำหนดให้

I13         =            (V1-V3)/z13

                                             =            (0.3755-0.3244)/j0.25

                                             =            -j0.2044

เมื่อ

V1          =            1-(j0.978/j0.1566)

                                             =            0.3755

V3          =            1-(j0.1058/j0.1566)

                                             =            0.3244

 

11.    สมมติว่าแรงดันก่อนที่จะเกิดความผิดพร่อง (Prefault  voltage) มีค่าเท่ากับ 1.0 ต่อหน่วย  จงคำนวณหาค่าแรงดันที่บัส 1 2 และ 3 ภายหลังจากการเกิดความผิดพร่องที่บัส 3 โดยใช้ข้อมูลอิมพีแดนซ์ผิดพร่อง (Failt impedance) และบัสอิมพีแดนซ์เมทริกซ์ต่อไปนี้

 = j0.16 p.u.   

1) 0.24 0.32 และ 0.68 pu.                              2) 0.35 0.47 และ 0.53 pu.

3) 0.65 0.53 และ 0.47 pu.                              4) 0.76 0.68 และ 0.32 pu.

เฉลย ข้อ4

วิธีทำ

 

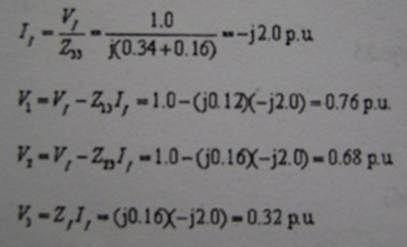
12.    เครื่องกำเนิดไฟฟ้าซิงโครนัสมีพิกัด 500 เมกะโวลต์แอมแปร์  20  กิโลโวลต์  50  เฮิรตซ์  ค่ารีแอคแตนซ์ในภาวะชั่วแวบ (Sub-transient reactance) เท่ากับ 0.15 ต่อหน่วยในขณะที่เครื่องกำเนิดไฟฟ้ากำลังจ่ายโหลดที่พิกัดกำแรงดัน  โดยมีพิกัดตัวประกอบกำลังแบบตาม (Lagging power factor) เท่ากับ 0.9 ได้เกดการลัดวงจรแบบสามเฟส (Three=phase short circuit) ขึ้นที่ขั้วของเครื่องกำเนิดไฟฟ้า จงคำนวณหาค่า rms ของกระแสสลับ

1) 90.8 แอมแปร์                                              2) 96.2 แอมแปร์

3) 103.3 แอมแปร์                                            4) 179.0 แอมแปร์

เฉลย ข้อ3

วิธีทำ

 

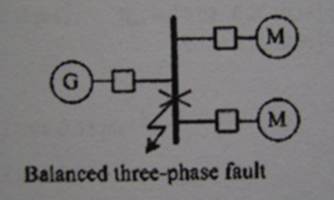
13.    เครื่องกำเนิดไฟฟ้าซิงโครนัสสามเฟสพิกัด 500 kVA 2.4 kV มีค่ารีแอคแตนซ์ Sub-transient เท่ากับ 0.2 pu. ต่อกับมอเตอร์ไฟฟ้าซิงโครนัสสามเฟสสองตัวขนานกันดังแสดงในรูปข้างล่างนี้

เมื่อใช้พิกัดของเครื่องกำเนิดไฟฟ้าเป็นค่าฐาน  มอเตอร์แต่ละตัวมีค่ารีแอคแตนซ์ Sub-transientเท่ากับ 0.8 pu. จงคำนวณหาค่า rms ของกระแสลัดวงจรที่เกิดขึ้น

1) 200 แอมแปร์                                               2) 347 แอมแปร์

3) 902 แอมแปร์                                               4) 1562 แอมแปร์

เฉลย ข้อ3

วิธีทำ

 

14.    กำหนดให้องค์ประกอบบางตัวในเมตริกซ์บัวอิมพิแดนซ์ของระบบที่พิจารณามีค่าดังนี้ Z11 = j0.28 pu.  Z22 = j0.25 pu. และ Z12 = j0.1 pu. ก่อนเกิด Three-phase  fault ที่บัสที่ 2 ของระบบ  พบว่า บัส1 มีขนาดแรงดันเท่ากับ 0.99  pu. บีส  2  มีขนาดแรงดันเท่ากับ 1 pu. ข้อใดต่อไปนี้กล่าวถูกต้อง

               1) บัส 1 มีค่า Short-circuit Capacity สูงกว่าบัส2

               2) กระแสลัดวงจรแบบสามเฟสที่บัส2 มีค่าเท่ากับ 4 pu

               3) หลังจากเกิดการลัดวงจรที่บัส2 แล้วขนาดของแรงที่บัส1  มีขนาดเท่ากับ 0.4 pu.

               4) ถูกทั้งข้อ ข และ ค

เฉลย ข้อ2

วิธีทำ

ขนาดกระแสลัดวงจรที่บัส2 เท่ากับ 1/Z22 = 4 pu.

ทำให้เกิดแรงดันตกที่บัส1 เท่ากับ 1/Z22 = 0.4 pu.

ดังนั้นขนาดของแรงดันที่บัส1 หลังการเกิดการลัดวงจร มีค่าเท่ากับ 0.99-0.4 = 0.59 pu.

บัส1 มีค่า S/C Capacity = (1/Z11)*Sbase ต่ำกว่า S/C Capacity ของบัส2

 

15.    กำหนดเมตริกซ์   ของระบบไฟฟ้ากำลังดังนี้

หากเกิดการลัดวงจรแบบสามเฟสขึ้น ที่บัส 3 ผ่านอิมพีแดนซ์ลัดวงจร   = j0.19 pu. จงคำนวณหาค่าแรงดันที่ บัส 1 บัส 2 และ บัส 3 ตามลำดับ

1) 0.925 pu. , 0.925 pu. , 0 pu.                                     2) 0.925 pu. , 0.925 pu. , 0.525 pu.

3) 0.925 pu. , 0.925 pu. , 0.925 pu.                             4) 0 pu. , 0 pu. , 0 pu.

เฉลย ข้อ2

วิธีทำ

V1          =             1-Z13/(Z33+Zf)

                                             =             1-j.03/(j.21+.19).

                                             =             0.925 p.u.

V2          =             1-Z23(Z33+Zf)

                                             =             1-j.03/(j.21+.19)

                                             =             0.925 p.u.

V3          =             If*Zf

                                             =             (1/(j.21+j.19))*j.19

                              =             0.525 p.u.

 

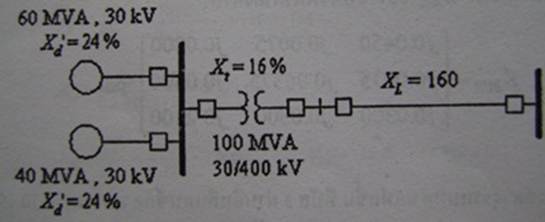
16.    พิจารณาระบบไฟฟ้ากำลังในรูป  ตอนเริ่มต้นอยู่ในสภาวะไร้โหลด  เครื่องกำเนิดไฟฟ้าทำงานที่แรงดันพิกัด  หากเกิดการลัดวงจรแบบสามเฟสขึ้นที่ปลายด้านรับของสายส่ง  จงคำนวณหาค่า Short-circuit MVA

 

 

1) 150 MVA                                                    2) 200 MVA

3) 250 MVA                                                    4) 300 MVA

เฉลย ข้อ2

วิธีทำ

 

17.    ระบบไฟฟ้า 4 บัส มีค่าบัสอิมพีแดนซ์เมตริกซ์  ลำดับที่ 1,2 และ 0 ดังแสดงด้านล่างเป็นค่าต่อหน่วย หากเกิดลัดวงจรแบบสามเฟสลงกราวน์ขึ้นในระบบที่บัส 3 จงหาขนาดแรงดันที่บัสที่ 1 ระหว่างเกิดการลัดวงจรดังกล่าวเป็นค่าต่อหน่วย(กำหนดให้ขนาดแรงดันก่อนเกิดลัดวงจรมีขนาดเป็น 1 p.u. ที่ทุกบัส)

 

 

 

 

 

 

1) 0.325 p.u.                                                     2) 0.465 p.u.

3) 0.535 p.u.                                                     4) 1.0 p.u.

เฉลย ข้อ3

 

 

วิธีทำ

กำหนดให้

V1          =            1-Z13/Z33

                                             =            1 – j.0789/j.1696

                                             =            0.5348 p.u.

ดังนั้น V1 มีค่าเป็น 0.5348

 

18.    ถ้าเกิดลัดวงจรแบบ 1 เฟส  ลงดิน(เฟส a) ณ บัส 1 ดังแสดงในรูปข้างล่างวิเคราะห์หาขนาดของกระแสลัดวงจรเฟส a ณ บัส 1 ถ้าในสถานะก่อนลัดวงจรแรงดันที่บัส 1 มีขนาด 1 เปอร์ยูนิต

 

 

 

 

1) 14.2857 เปอร์ยูนิต                                                     2) 11.7647 เปอร์ยูนิต

3) 9.5238 เปอร์ยูนิต                                                       4) 3.9216 เปอร์ยูนิต

เฉลย ข้อ2

วิธีทำ

 

 

 

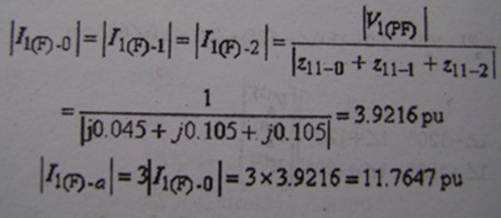
19.    จงคำนวณหาแรงดันที่ในเฟส b และ c () จากข้อมูลต่อไปนี้

 

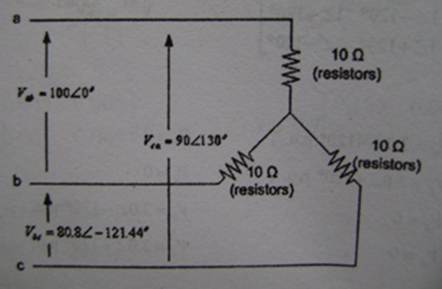
20.    จากรูปวงจร  และค่าแรงดันระหว่างสายที่กำหนด  จงหาค่าของ    โดยอาศัยหลักการ  Symmetrical  Components

 

1)   = 4.609 – j2.358A                          2)   = 0.654 – j0.060A

3)   = 8.957 – j0.454A                          4) ไม่มีข้อใดถูก

เฉลย ข้อ1

วิธีทำ

     =             /Zdelta

Zdelta    =             3*Zy

                                             =             30

    =             1/3*(Vab+a*Vab+a*a*Vca)

    =             /*(cos30+j sin 30)

     =             3*/ Zdelta

จะได้

     =             4.609 – j2.358 A

  ติดต่อสอบถาม/สั่งซื้อแนวข้อสอบ

 Line ID : Panisara_test